Cześć!
W tym artykule chciałbym przedstawić Wam świat, w którym wszyscy żyjemy w nieco innym świetle. Kryptografia, jest to pojęcie o którym wiele osób słyszało, jednak nie dostrzega go na co dzień. Mam nadzieję to zmienić i pokazać Wam jej podstawowe narzędzia.
Zazwyczaj pierwsze skojarzenia odnośnie kryptografii dotyczą świata militariów – często myślimy o wojnie, enigmie i szpiegach przesyłających tajne depesze. Prawda jest jednak zupełnie inna. Obecnie, w dobie Internetu, w świecie cywilnym ma ona o wiele szerszą liczbę zastosowań niż było to we wcześniejszych wiekach. Zanim podam Wam ich przykłady musimy ustalić jakie są jej podstawowe cele.
Często w kręgu osób zainteresowanych bezpieczeństwem w tym miejscu mówi się o modelu zwanym triadą CIA. Wiem o czym myślicie ale nie, nie ma ona nic wspólnego ze słynną amerykańską agencją wywiadowczą a z oczekiwanymi własnościami informacji:
- Confidentiality – poufność, tylko określone osoby są w stanie zrozumieć informację,
- Integrity – integralność, wszelkie manipulacje informacją muszą zostać wykryte przez odbiorcę,
- Availability – dostępność, dostęp do informacji musi być uwierzytelniony.
Triada CIA opisuje cele, które uzyskujemy dzięki kryptografii. Najpowszechniejszym miejscem, w którym stykamy się z kryptografią jest Internet.
Gdzie jest kryptografia w naszym życiu?
Kilka lat temu, tuż po tym, gdy zapłaciłem za wizytę dentystyczną, mój lekarz zadał jedno pytanie – „Przepraszam, czy nie jest Pan przypadkiem informatykiem?”. Zapaliła mi się z tyłu głowy obawa przed syndromem darmowego informatyka (który zawsze i wszędzie udziela bezpłatnej pomocy) ale jednak chęć pomocy zwyciężyła, zwłaszcza, że chwilę wcześniej uratował mnie od wielkiego bólu zęba, więc odpowiedziałem zgodnie z prawdą.
Dzień wcześniej otworzył bowiem załącznik, który miał być fakturą a okazał się wirusem. Lekarz zaobserwował jeden objaw. Próba odwiedzenia poczty Google’a oraz kalendarza kończyła się komunikatem „Twoje połączenie nie jest prywatne”. Historię zwieńczyło pytanie, czy da się ominąć komunikat i przejść do usług Google’a pomimo braku szyfrowania. Niestety odpowiedź powinna brzmieć, tak ale nie należy z niej korzystać. Prawda jest taka, że większość usług, z których korzystamy w Internecie jest szyfrowana. Poniżej możecie porównać w jaki sposób wyglądają informacje wysyłane przez naszą przeglądarkę do strony internetowej z szyfrowaniem i bez.
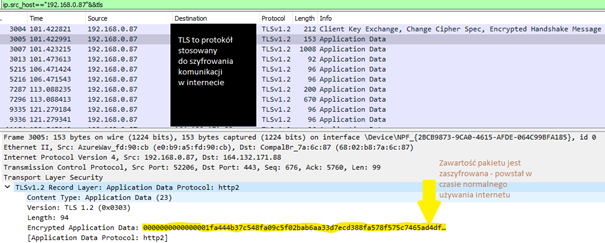
Zrzut ekranu zawiera przykładowy zapis transmisji poprzez Wi-Fi gdzie komunikacja jest szyfrowana. Możecie zauważyć drobną wzmiankę, że wykorzystywany jest protokół HTTP2, który jest ukryty poprzez TLS’a. Nie szyfrowana komunikacja wygląda natomiast tak:
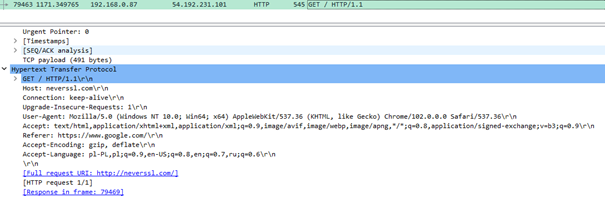
Sekcja Hypertext Transfer Protocol zawiera niezaszyfrowany ładunek informacji.
Kolejnym przykład kryptografii w naszych domach stanowią routery. Komunikacja pomiędzy urządzeniami w sieciach Wi-Fi nie zawsze przebiega bez zakłóceń. Dzięki niej jesteśmy np. w stanie wykryć przynajmniej część przekłamań w transmisji. Protokół TCP (schemat komunikacji wykorzystywany do łączności z Internetem) wymaga stosowanie dodatkowych kodów aby zapewnić integralność transmisji.
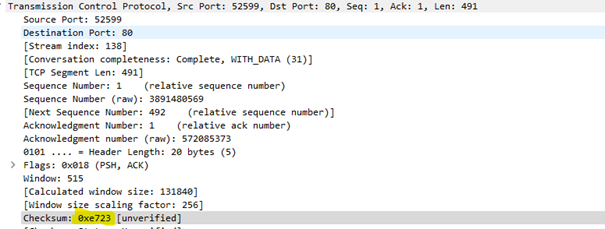
Sumy kontrolne (zakreślone żółtym podkreślaczem pole Checksum) pozwalają wykryć nieprawidłowe pakiety w sieci – może do tego dojść z wielu różnych powodów jak np. zbyt słabego sygnału czy przeszkody fizyczne takie jak ściany.
W jaki sposób zaszyfrować wiadomość?
Teraz, kiedy mamy pewne wyobrażenia dotyczące kryptografii w życiu codziennym chciałbym dać Wam pewien przedsmak tego czym będziemy zajmować się w kolejnych artykułach. Zaczniemy więc od problemu szyfrowania na przykładzie szyfru Cezara – miał być on używany przez niego do poufnej komunikacji ze swoimi przyjaciółmi. Ciekawe, czy również z Brutusem…
Opowiem Wam zaraz pewną bajkę. Musicie wiedzieć, że bajki kryptograficzne mają pewien element wspólny z komediami romantycznymi. W obu gatunkach mamy dwóch głównych bohaterów, w życiu których pojawia się trzecia, która odkąd się pojawiła to miesza
w zaistniałej wcześniej sytuacji. Bohaterowie naszej bajki nazywają się Juliusza Cezar, Marek Krassus oraz Gnejusz Pompejusz. Istnieli jak pewnie wiecie naprawdę, ale historia ta została całkowicie zmyślona.
Dawno, dawno temu, za siedmioma lasami, za siedmioma górami… No dobrze, w starożytnym Rzymie , istniał sojusz trzech wielkich mężów – wymienionego wcześniej Juliusza, Gnejusza i Marka. Trudno mówić w ich przypadku o wielkiej miłości (całe szczęście) a nawet przyjaźni. Najbliżej tej relacji do czegoś w rodzaju małżeństwa z rozsądku. Otóż Marek wybierał się na wojnę z Partami i zastanawiał się w jaki sposób informować Cezara o postępach kampanii tak żeby ani Gnejusz, ani Asteriks i Obeliks z odległej Galii przechwyciwszy wiadomość nie potrafili jej zrozumieć.

Juliusz-kryptograł pomyślał sobie: „Kurcze, przecież musi dać się jakoś tak zmodyfikować tekst żeby nie dało się go zrozumieć a później odwrócić ten proces…”. Myślał nad tym problemem kilka dni aż w końcu wymyślił! Czemu by nie przesuwać liter alfabetu o 3, tj. zamieniać litery A na D, B na E, C na F, itd ….? Przecież ten proces da się odwrócić! Jak pomyślał tak zrobił.
| Tabela przekształceń | ||||||||||||||||||||||||||
| Przed przekształceniem | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | W | V | X | Y | Z |
| Po przekształceniu | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | W | V | X | Y | Z | A | B | C |
Przykład:
Tekst jawny: ALA MA KOTA
Tekst poufny: DOD PD NRVD
Wiadomość, po przesunięciu liter o 3 podobna sama do siebie za bardzo nie była, natomiast po odwróceniu procesu na uzyskanej wiadomości uzyskał oryginalną. Voila! Problem rozwiązany.
Dzisiaj proces pierwszy nazywamy szyfrowaniem, gdyż służy on transformacji tekstu jawnego (plaintext) w tzw. szyfrogram (ciphertext, tekst poufny) z wykorzystaniem pewnego klucza (w przypadku szyfru Cezara jest nim wielkość przesunięcia). Proces odwrotny tj. transformacja szyfrogramu w tekst oryginalny nazywamy natomiast deszyfracją. W kolejnych artykułach przekonacie się, że klucz szyfrowania i deszyfrowania nie muszą być koniecznie takie same. Matematyk powiedział by, że szyfrowanie i deszyfrowanie są to takie funkcje Encrypt i Decrypt, że:
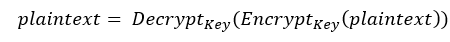
Wszystko ładnie i pięknie, Cezar z Krassusem czuli się w pełni komfortowo i bezpiecznie, do tego stopnia, że poruszali nawet bardziej intymne tematy. Czy słusznie?
Tutaj pojawia się trzeci bohater, gnuśny (a przynajmniej na potrzeby tej opowieści) Gnejusz, który przechwycił wiadomość. Spojrzał i na pierwszy rzut oka nic nie rozumie… Trochę tak,
jak w piosence Voulez-vous coucher avec moi zespołu Aquarium:
Trzymam w mym ręku list, ale widzę tylko litery
Boris GrebensHchikov – Voulez-Vous coucher avec moi
Nie pamiętam nawet, jak złożyć z nich słowa.
Mimo wszystko Gnejusz okazał się być szczwanym lisem, pomyślał: „Alfabet łaciński nie jest taki długi, to tylko 26 liter…”, poza tym podsłuchał kiedyś gdy dwaj „przyjaciele” rozmawiali o jakimś przesunięciu… Wziął wszystkich swoich 25 greckich niewolników, którzy uczyli jego dzieci matematyki i kazał każdemu z nich postąpić tak: pierwszy niewolnik zamieniał B na A, drugi C na A itd…. Odkrył, że ten podstawiający z przesunięciem o 3 stworzył sensowny tekst. Sekrety Juliusza Cezara oraz Marka Krassusa nie były już dłużej bezpieczne.
W XIX wieku holenderski kryptograf Auguste Kerckhoffs ukuł kilka zasad, które można streścić w zdaniu bezpieczeństwo systemu kryptograficznego powinno być oparte na tajności klucza a nie procedur. Poza tym przestrzeń kluczy powinna być na tyle duża by nie można było ich efektywnie sprawdzić poprzez przegląd wszystkich możliwości jak to zrobił nasz Gnejusz.
Pojawia się w tym momencie kolejne pytanie, czy gdybyśmy zamiast przesunięć stworzyli losową tablicę podmian znaków byłoby to trudniejsze do złamania? W końcu takich tablic jest 26! (26 * 25 * … * 1) czyli 403 291 461 126 605 635 584 000 000, czyli chyba więcej niż dzisiaj jest mieszkańców globu. Na ówczesne czasy chyba tak, na dzisiejsze już nieco mniej.
Dla każdego języka charakterystyczną cechą jest prawdopodobieństwo z jakim występują różne litery – nazywamy to po angielsku footprint’em. Jeśli przeanalizujemy nawet takie losowe przyporządkowanie to dla stosownych znaków, proporcje zostaną zachowane i łatwo możemy odzyskać tabelę przekształceń.
| Sen nocy letniej | Hamlet | Tytus Andronikus | Juliusz Cezar |
| e – 0.125070 t – 0.089611 o – 0.082563 a – 0.073165 i – 0.067040 n – 0.064873 r – 0.063607 s – 0.062375 h – 0.060174 l – 0.042804 d – 0.037934 u – 0.034204 m – 0.030064 y – 0.025354 w – 0.023495 c – 0.022468 f – 0.019651 g – 0.018613 p – 0.018237 b – 0.015545 v – 0.009261 k – 0.008850 j – 0.001688 q – 0.001437 x – 0.001380 z – 0.000160 | e – 0.119177 t – 0.094475 o – 0.090922 a – 0.072433 i – 0.070513 n – 0.066361 s – 0.061381 r – 0.061328 h – 0.058782 l – 0.041492 d – 0.035600 u – 0.031561 m – 0.028901 c – 0.025002 f – 0.024669 y – 0.021922 w – 0.020429 g – 0.019023 p – 0.018363 b – 0.013724 v – 0.009891 k – 0.008652 x – 0.001613 q – 0.001586 j – 0.001520 z – 0.000387 | e – 0.116557 t – 0.091163 o – 0.079234 a – 0.076153 s – 0.070158 r – 0.066631 i – 0.066056 n – 0.063976 h – 0.062430 l – 0.042079 d – 0.040791 u – 0.039810 m – 0.031577 y – 0.023036 w – 0.022481 c – 0.022115 f – 0.018478 b – 0.016279 p – 0.015238 g – 0.015040 v – 0.010047 k – 0.006777 x – 0.001496 j – 0.001120 q – 0.000941 z – 0.000337 | e – 0.111776 t – 0.090989 o – 0.079855 a – 0.078732 s – 0.074840 i – 0.069186 r – 0.064229 n – 0.062292 h – 0.054276 u – 0.043762 l – 0.039957 d – 0.037449 c – 0.029907 m – 0.026944 y – 0.023323 w – 0.021900 f – 0.019925 b – 0.018240 g – 0.016004 p – 0.015713 v – 0.009188 k – 0.007784 j – 0.001249 x – 0.001046 z – 0.001026 q – 0.000397 |
| Otello | Król Lear | Makbet | Romeo i Julia |
| e – 0.118021 o – 0.093300 t – 0.089555 a – 0.075691 i – 0.072920 s – 0.064400 n – 0.062901 h – 0.059833 r – 0.056231 l – 0.044050 d – 0.040107 u – 0.031610 m – 0.029905 c – 0.023494 y – 0.023396 w – 0.021660 f – 0.020160 g – 0.020030 p – 0.015265 b – 0.014678 v – 0.010811 k – 0.008557 j – 0.001355 x – 0.001226 q – 0.000624 z – 0.000206 | e – 0.123370 t – 0.091010 o – 0.082386 a – 0.074466 r – 0.066092 n – 0.064729 i – 0.061943 s – 0.061511 h – 0.059232 l – 0.045270 d – 0.040576 u – 0.033572 m – 0.028211 c – 0.024047 y – 0.023805 w – 0.023063 g – 0.021867 f – 0.021526 p – 0.015605 b – 0.014197 k – 0.010820 v – 0.009252 j – 0.001355 x – 0.001287 q – 0.000606 z – 0.000197 | e – 0.136079 t – 0.091050 o – 0.078711 a – 0.075283 n – 0.063903 s – 0.063343 h – 0.062361 i – 0.060133 r – 0.058979 l – 0.042537 d – 0.039887 u – 0.035202 m – 0.029912 c – 0.026279 w – 0.023548 y – 0.022760 f – 0.020612 g – 0.018212 b – 0.017812 p – 0.014785 k – 0.009038 v – 0.004879 x – 0.002342 q – 0.001497 j – 0.000514 z – 0.000343 | e – 0.119085 t – 0.092119 o – 0.082889 a – 0.076255 i – 0.065469 r – 0.064054 n – 0.062439 h – 0.061715 s – 0.061532 l – 0.044045 d – 0.037029 u – 0.034058 m – 0.031761 y – 0.024470 w – 0.023845 c – 0.022922 f – 0.020649 g – 0.018860 b – 0.016862 p – 0.016563 v – 0.009755 k – 0.008240 j – 0.003129 x – 0.001332 q – 0.000633 z – 0.000291 |
Jako próbkę danych wykorzystałem oryginalne teksty różnych sztuk Szekspira ze strony projektu Guttenberg. Możecie zauważyć, że statystyki wyglądają dość podobnie. Im dłuższy tekst próbujecie zdeszyfrować, tym dokładniej będzie działać odtworzona tablica. Na stronie repozytorium https://gitlab.com/sisiphus-on-code/cryptography, w katalogu caesar-cipher znajdziecie źródła do programów wykorzystanych do statystyk, testowe pliki oraz eksperyment z deszyfrowaniem bazując na statystykach występowania znaków.
Możecie zauważyć w tym miejscu, dwa typy problemów:
- W jaki sposób zabezpieczyć poufność komunikacji?
- W jaki sposób możemy przeanalizować przechwycone informacje aby odzyskać lub podmienić chociaż część danych nie znając klucza?
Na pierwsze pytanie odpowiada kryptografia a na drugie kryptoanaliza a oba zagadnienia są przedmiotem nauki o nazwie kryptologia.
Jakie narzędzia zapewnia nam kryptografia
Teraz kiedy zobaczyliście przykład w jaki sposób możemy (chociaż może nieco nieudolnie,
w kolejnych artykułach przedstawię Wam lepsze sposoby) zapewniać poufność korespondencji, pewnie jesteście ciekawi co jeszcze będzie elementem naszego narzędziowego przybornika.
Poniżej znajdziecie krótkie zastawienie narzędzi, które zobaczycie w kolejnych wpisach:
| Narzędzie | Opis i zastosowanie |
| Algorytmy szyfrowania | Algorytmy, które umożliwiają odwracalne zmodyfikowanie zawartości wiadomości aby uniemożliwić jej odczytanie. |
| Podpisy cyfrowe | Protokoły wykorzystujące algorytmy szyfrowania asymetrycznego (tj. klucz szyfrowania jest inny od klucza deszyfrowania) aby umożliwić potwierdzenie np. kto jest nadawcą wiadomości. |
| Funkcje hashujące (skrótu) | Przypisanie większemu pakietowi informacji charakterystycznej wartości liczbowej o stałym rozmiarze w sposób nieodwracalny. |
| Kody korekcyjne | Dodatkowa informacja dodawana do wiadomości dzięki której gdy pojawiły się przekłamania transmisji wiadomość można próbować odzyskać. |
| (H)MAC – kody uwierzytelnienia wiadomości | Algorytmy zapewniające integralność wiadomości (nie muszą zapewniać pewności, kto nadał daną wiadomość). |
Wszystkie te narzędzia są łączone w większą całość – bardziej skomplikowane protokoły
i kryptosystemy. U ich podstaw natomiast leżą pewne zagadnienia związane z matematyką tj. liczby losowe, problemy teorio-liczbowe (np. problem dyskretnego logarytmu albo rozkładu liczb na czynniki pierwsze), kombinatoryka i rachunek prawdopodobieństwa.
W kolejnych wpisach postaram się przybliżyć Wam szczegóły w jaki sposób działają powyższe narzędzia a tymczasem najwyższy czas kończyć na dziś!
Do zobaczenia 😊
